Wir haben nun das Instrumentarium beieinander, ein erstes, wenn auch noch
recht einfaches Ex-ante-Modell unserer Modellwirtschaft zu konstruieren,
mit dem wir im ![]() nächsten
Abschnitt sogar schon Simulationsrechnungen werden durchführen können.
Unsere Markoökonomie besteht momentan nur aus dem Gütermarkt. Zudem
unterstellen wir "autonome Investitionen". Wie beim
nächsten
Abschnitt sogar schon Simulationsrechnungen werden durchführen können.
Unsere Markoökonomie besteht momentan nur aus dem Gütermarkt. Zudem
unterstellen wir "autonome Investitionen". Wie beim ![]() Sparen und
beim
Sparen und
beim ![]() Konsum signalisiert
das Adjektiv "autonom" auch
hier, dass wir die Investitionen als exogene Größe auffassen.
Wir gehen zunächst davon aus, dass die Unternehmen ihre Investitionsentscheidungen
bereits getroffen haben und in der betrachteten Periode Iaut investieren
wollen und sich davon durch nichts abbringen lassen.
Konsum signalisiert
das Adjektiv "autonom" auch
hier, dass wir die Investitionen als exogene Größe auffassen.
Wir gehen zunächst davon aus, dass die Unternehmen ihre Investitionsentscheidungen
bereits getroffen haben und in der betrachteten Periode Iaut investieren
wollen und sich davon durch nichts abbringen lassen.
Unser Modell besteht damit aus drei Gleichungen: der Konsumfunktion, der "Investitionsfunktion" und
der Einkommensidentität. Die Konsumfunktion und die Investitionsfunktion
sind Verhaltensgleichungen, da sie Entscheidungen - also Verhalten - von
Wirtschaftssubjekten beschreiben. Die Investitionsfunktion tut dies momentan
noch auf eine rudimentäre Art und Weise: die Unternehmen investieren
Iaut, basta. Die Einkommensidentität ist eine ![]() Definitionsgleichung der
VGR.
Definitionsgleichung der
VGR.
[1] C = Caut + cY
[2] I = Iaut
[3] Y = C + I
Alle drei Gleichungen finden wir in Abbildung 1 wieder, die der Anschaulichkeit
wegen das bisherige Zahlenbeispiel fortführt. Die ![]() Konsumfunktion haben
wir bereits ausführlich erörtert. Da jetzt auch die Investitionen
im Diagramm dargestellt werden, ist an der Ordinate das Symbol I hinzu gekommen.
Die autonomen Investitionen sind mit 100 angenommen. Die Investitionsfunktion
ist eine Parallele zur Abszisse, da die Investitionen von der Höhe der
Einkommen unabhängig sind.
Konsumfunktion haben
wir bereits ausführlich erörtert. Da jetzt auch die Investitionen
im Diagramm dargestellt werden, ist an der Ordinate das Symbol I hinzu gekommen.
Die autonomen Investitionen sind mit 100 angenommen. Die Investitionsfunktion
ist eine Parallele zur Abszisse, da die Investitionen von der Höhe der
Einkommen unabhängig sind.
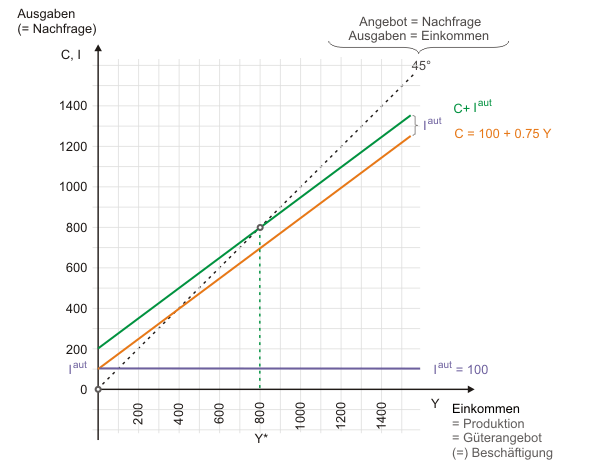
Das Gleichgewicht bei autonomen Investitionen: Die Nachfrage nach Konsum- und Investitionsgütern stimmt beim Gleichgewichtseinkommen Y* mit dem Güterangebot überein.
Gleichung [3] beschreibt das Modellgleichgewicht. Das wäre vielleicht etwas deutlicher zu erkennen, wenn nicht in [3] auf eine Kennzeichnung der Variablen als geplante Größen verzichtet worden wäre. Das bequeme Weglassen von Indizes ist unter Ökonomen aber (leider?) üblich. Die ausführliche Schreibweise ist
[3a] Ygepl = Cgepl + Igepl (oder: AS = AD)
Bei [3] handelt es sich also streng genommen gar nicht mehr um die Definitionsgleichung aus der VGR, die immer erfüllt sein muss, sondern um eine verkürzte Schreibweise der Gleichgewichtsbedingung [3a]. Wenn sie erfüllt ist, befindet sich die Wirtschaft im Gleichgewicht, wenn aber
[3b] Ygepl > Cgepl + Igepl ,
ist das Güterangebot größer als die Nachfrage, und wenn
[3c] Ygepl < Cgepl + Igepl ,
bleibt das Angebot hinter der Nachfrage zurück.
Um das Gleichgewichtseinkommen analytisch zu bestimmen, setzt man die Konsum- und die Investitionsfunktion in die Gleichgewichtsbedingung ein:
[4] Y = Caut + cY + Iaut
[5] Y-cY = Caut + Iaut
[6] (1-c)Y = Caut + Iaut
![]() [7]
[7] ![]() (Gleichgewichtseinkommen)
(Gleichgewichtseinkommen)
Das Gleichgewichtseinkommen Y* hängt allein von den Modellparametern
autonomer Konsum, autonome Investitionen und marginale Konsumquote ab. Die
Höhe der gesamtwirtschaftlichen Produktion wird demnach allein durch
die (Konsum- und Investitions)Nachfrage bestimmt. Die drei Parameter
können
als bekannt vorausgesetzt werden. Die marginale Konsumquote und der autonome
Konsum lassen sich über die ![]() Schätzung
der Konsumfunktion ermitteln.
Für die Höhe der autonomen Investitionen kann man die VGR heranziehen.
Das Gleichgewichtseinkommen kann also bestimmt werden - im Prinzip jedenfalls.
Für eine praktische Simulations- oder Prognoserechnung eignet sich
dieses rudimentäre Modell natürlich nicht.
Schätzung
der Konsumfunktion ermitteln.
Für die Höhe der autonomen Investitionen kann man die VGR heranziehen.
Das Gleichgewichtseinkommen kann also bestimmt werden - im Prinzip jedenfalls.
Für eine praktische Simulations- oder Prognoserechnung eignet sich
dieses rudimentäre Modell natürlich nicht.
Für die grafische Lösung müssen der Konsum und die Investitionen zur grün dargestellten Gesamtnachfrage C+I addiert werden. Diese Funktion erhält man, indem man die Konsumfunktion um den Betrag der Investitionen (hier immer 100) nach oben verlagert, d.h. die Funktionswerte beider Funktionen für jedes Einkommen addiert. Der Gleichgewichtsbedingung [3a] (AS = AD) entspricht im Diagramm die 45°-Linie. Die linke Seite dieser Gleichung (Ygepl) lesen wir an der Abszisse ab, die rechte Seite (Cgepl + Igepl) an der Ordinate.
Die Abbildung lässt erkennen, dass das gesamtwirtschaftliche Angebot mit der gesamtwirtschaftlichen Nachfrage bei einem Einkommen von 800 übereinstimmt. Der optische Eindruck lässt sich durch Einsetzen der Parameterwerte in die analytische Lösung [7] bestätigen:
[8] ![]()
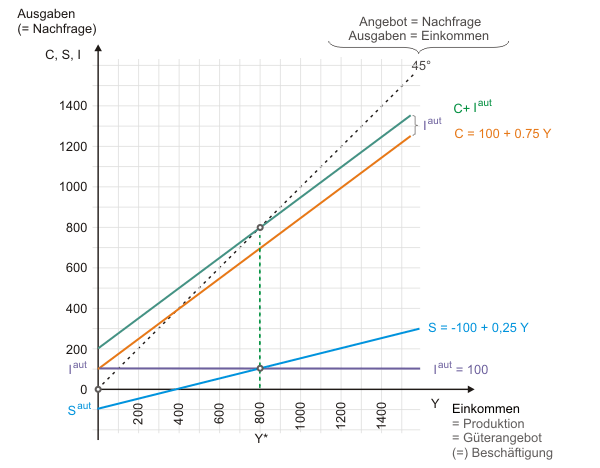
Das gesamtwirtschaftliche Güterangebot entspricht der Nachfrage, wenn das geplante Sparen mit dem geplanten Investitionsvolumen übereinstimmt. [Maussensitive Grafik: Um das Gleichgewicht grafisch zu bestimmen, genügen Spar- und Investitionsfunktion.]
Aus unseren Überlegungen zum Wirtschaftskreislauf wissen wir, dass im gesamtwirtschaftlichen Gütermarktgleichgewicht "Sparen gleich Investieren" gilt. Abbildung 2 wurde deswegen gegenüber Abbildung 1 um die Sparfunktion ergänzt und wir finden mit der Methode des genauen Hinschauens bestätigt, dass Sparen und Investieren wie erwartet beim Gleichgewichtseinkommen übereinstimmen.
Analytisch hätten wir das Gleichgewicht also auch wie folgt bestimmen können:
[9] S = I (besser wäre eigentlich: Sgepl = Igepl)
[10] Saut + sY = Iaut
[11] sY = -Saut + Iaut
[11] ![]()
Die Farbgebung verdeutlicht, dass sich die Gleichungen [11]
und [7] im Grunde nicht unterscheiden, da die gleichfarbigen Größen
jeweils miteinander ![]() übereinstimmen.
übereinstimmen.
Gleichung 9 ermöglicht dem geübten Anwender übrigens eine sehr zügige grafische Bestimmung des Gleichgewichtseinkommens. In einem vorbereiteten Einkommen-Ausgaben-Diagramm (s. maussensitive Abb. 2) genügen ihm zwei Striche. Der erste Strich ist die Sparfunktion, der zweite die Investitionsfunktion. Der Schnittpunkt zeigt das Gleichgewichtseinkommen.
Da das Modell nicht dynamisch angelegt ist*, lassen sich über Anpassungsprozesse nur Vermutungen anstellen. Dazu dient Abbildung 3.
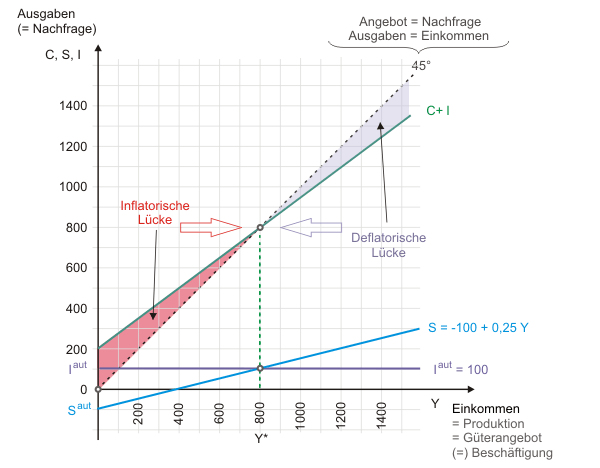
Das Gütermarktgleichgewicht ist stabil, da die Produktion bei einem Nachfrageüberschuss ausgedehnt und bei einem Angebotsüberschuss vermindert wird.
Im rot schattierten Bereich übersteigt die gesamtwirtschaftliche Nachfrage (C+I) die Produktion (Y). Sofern die Unternehmen über freie Kapazitäten verfügen, werden sie ihre Produktion ausdehnen. Das bedeutet, dass sich die Produktion in Richtung des roten Pfeils, also in Richtung auf das Gleichgewichtseinkommen verlagert.
Im lila schattierten Bereich ist ein Überschussangebot zu beobachten. Die Unternehmen werden ihre Ware nicht los und schränken die Produktion daher ein. Auch hier beobachten wir mit dem lilafarbenen Pfeil eine Bewegung in die richtige Richtung. Wir können also Hoffnung haben, dass das Gleichgewicht stabil ist.
Da in den schattierten Bereichen eine Lücke zwischen Angebot und Nachfrage
klafft, spricht man in Anlehnung an die mikroökonomische Preistheorie
von einer inflatorischen oder deflatorischen Lücke. Ein Nachfrageüberschuss
auf einem Markt führt nach der ![]() walrasianischen
Preisanpassungshypothese zu Preissteigerungen, ein Angebotsüberschuss
zu Preissenkungen. Entsprechende Reaktionen werden für das Preisniveau
vermutet. Kommt es allgemein zu Nachfragelücken, dann werden sich die
Preissenkungen auf den einzelnen Märkten in einem sinkenden Preisniveau
niederschlagen. Herrscht hingegen auf der Mehrzahl der Märkte Angebotsknappheit,
so werden die auf breiter Front steigenden Preise das Preisniveau nach oben
ziehen.
walrasianischen
Preisanpassungshypothese zu Preissteigerungen, ein Angebotsüberschuss
zu Preissenkungen. Entsprechende Reaktionen werden für das Preisniveau
vermutet. Kommt es allgemein zu Nachfragelücken, dann werden sich die
Preissenkungen auf den einzelnen Märkten in einem sinkenden Preisniveau
niederschlagen. Herrscht hingegen auf der Mehrzahl der Märkte Angebotsknappheit,
so werden die auf breiter Front steigenden Preise das Preisniveau nach oben
ziehen.
Diese Aussagen beruhen auf Plausibilitätsüberlegungen. Das Modell
berücksichtigt das Preisniveau bisher in keiner Weise, sondern geht
ganz im Gegenteil von einem ![]() fixen
Preisniveau aus.
fixen
Preisniveau aus.
Von besonderem Interesse ist die deflatorische Lücke, die mit der eingangs
beschriebenen ![]() Grundposition
der keynesianischen Theorie - man könnte
auch formulieren: mit dem keynesianischen Glaubensbekenntnis - korrespondiert.
Die deflatorische Lücke zeichnet sich nämlich durch Unterbeschäftigung
aus.
Grundposition
der keynesianischen Theorie - man könnte
auch formulieren: mit dem keynesianischen Glaubensbekenntnis - korrespondiert.
Die deflatorische Lücke zeichnet sich nämlich durch Unterbeschäftigung
aus.
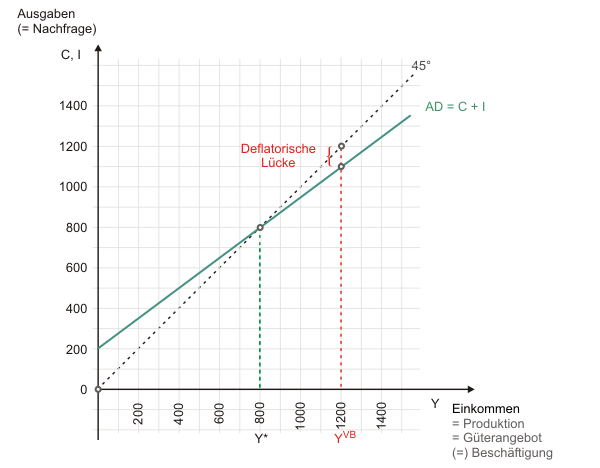
"Gleichgewicht bei Unterbeschäftigung": Die deflatorische Lücke begründet Unterbeschäftigung mit einem Mangel an Nachfrage.
Wir betrachten dazu Abbildung 4 und machen Gebrauch von der Überlegung,
dass wir an der Abszisse nicht das Einkommen, sondern indirekt auch die![]() Beschäftigung
ablesen können, da ein höheres Einkommen mit einer höheren
Beschäftigung einhergeht. Jetzt sei angenommen, dass Vollbeschäftigung
bei einem Einkommen von YVB=1200 herrschen würde.
Beschäftigung
ablesen können, da ein höheres Einkommen mit einer höheren
Beschäftigung einhergeht. Jetzt sei angenommen, dass Vollbeschäftigung
bei einem Einkommen von YVB=1200 herrschen würde.
Die Unternehmen würden eine Produktion in dieser Höhe planen, wenn sie damit rechnen würden, dass sie sie auch absetzen könnten. Bei einem Einkommen von 1200 beträgt die gesamtwirtschaftliche Nachfrage AD aber nur 1100, da die Haushalte 1000 zu Konsum- und die Unternehmen 100 zu Investitionszwecken nachfragen. Die Unternehmen werden die Nachfragelücke (= deflatorische Lücke) in Höhe von 100 nicht dauerhaft auf Lager produzieren wollen. Sie werden ihre Produktion also vermindern. Die Beschäftigung sinkt, das Einkommen sinkt. Erst wenn die Produktion auf 800 gefallen ist, steht dem Güterangebot eine gleich hohe Nachfrage gegenüber. Der Gütermarkt ist im Gleichgewicht, aber es herrscht Arbeitslosigkeit - das berühmte "Gleichgewicht bei Unterbeschäftigung". Zusammengefasst:
Ursache der Arbeitslosigkeit ist die Nachfragelücke.
Der Terminus Gleichgewicht bei Unterbeschäftigung ist eigentlich ein Widerspruch in sich. Unterbeschäftigung heißt ja gerade, dass der Arbeitsmarkt im Ungleichgewicht ist. Zudem sind die Kapazitäten der Unternehmen nicht ausgelastet.
Was zum Ausdruck kommen soll, dürfte aber klar sein: Der Gütermarkt befindet sich in einer stabilen Situation. Von ihm werden keine Impulse ausgehen, da die Unternehmen keinen Anlass sehen, ihre Produktion zu erhöhen. Wenn die Produktion nicht erhöht wird, wird auch das Einkommen nicht steigen. Das wäre aber notwendig, damit zusätzliche Nachfrage induziert wird. Eine - scheinbar? - ausweglose Situation:
Die Unternehmen produzieren nicht, weil es an Nachfrage fehlt, und die Haushalte fragen nicht nach, weil es an Einkommen fehlt.
... und an Einkommen fehlt es, weil nicht genug produziert wird. Damit kein falscher Eindruck entsteht - das Modell schließt Voll- und Überbeschäftigungssituationen keineswegs aus. Wenn zu den herrschenden Löhnen weniger Menschen arbeiten wollten, so dass das Vollbeschäftigungseinkommen gerade bei Y* (im Zahlenbeispiel 800) läge, wären sowohl der Güter- als auch der Arbeitsmarkt im Gleichgewicht. Würde das Arbeitsangebot noch geringer ausfallen, befände sich die Wirtschaft in einer inflatorischen Lücke, einer Situation des Aufschwungs mit einem Mangel an Arbeitskräften.
Blicken wir etwas über den Rand des Modells hinaus. Wird das Preisniveau fallen und auf diesem Weg zusätzliche Nachfrage entstehen, wenn wegen der defizitären Nachfrage Arbeitslosigkeit herrscht?
Die Verfechter dieses Modells würden argumentieren, dass das kein Ausweg wäre. Der Gütermarkt ist bei Y* im Gleichgewicht. Warum sollte das Preisniveau fallen? Dafür gibt es keinen Grund, denn die Unternehmen setzen ihre Produktion zu den herrschenden Preisen ab.
Ja, aber was ist denn mit den Löhnen? Wenn Arbeitslosigkeit herrscht, müssten die Unternehmern die Chance doch beim Schopf ergreifen und Arbeitskräfte zu geringeren Löhnen rekrutieren - mal angenommen, dass die Gewerkschaften es zuließen.
Die Keynesianer werden dem entgegenhalten, dass sinkende Löhne nicht zu mehr Beschäftigung führen würden. Die Höhe der Löhne ist nämlich ihrer Auffassung nach nicht die Ursache der Arbeitslosigkeit. Ursache ist die fehlende Nachfrage, die durch sinkende Löhne aber kaum steigen wird.* Das Gegenteil wäre zu befürchten. Durch psychologische Effekte verstärkt würden fallende Löhne zu noch größerer Zurückhaltung beim Konsum führen. Neue Autos kaufen die Bürgerinnen und Bürger, wenn die Einkommen steigen, nicht wenn sie fallen.